Technological pathways for cost-effective steel decarbonization

Plant-level pathway design model

This study developed a plant-level net-zero pathway model for the steel sector, called NZP-steel, to identify cost-effective technology pathways for each plant worldwide. The model integrates bottom-up modules built on plant-level datasets with top-down constraints, including national carbon-neutrality targets, rising steel demand and limited scrap supply.

The model consists of six modules (Extended Data Fig. 1). Three bottom-up modules are used to: (1) compile two plant-level industry datasets (yellow box), (2) calculate carbon emissions by plant and technology (blue box), and (3) estimate dynamic costs of decarbonization technologies (pink box). The algorithms for these modules are described below. The top-down module (green box) incorporates scenario constraints for plant-level pathway exploration, including national net-zero targets, future steel demand and scrap availability, sourced from the literature^7,46. Using plant-level cost and emission data from the bottom-up modules together with top-down constraints, the model determines the least-cost technology choice for each plant (cyan box). The resulting plant-level pathways are then aggregated to national, regional and global levels to quantify overall CO₂ abatement potentials and costs (purple box).

Plant-level datasets of global steel production and cost

The two plant-level databases used in this study are the World Crude Steel Capacity and Production Database³⁸ and the Global Iron and Steel Cost Database⁴⁷.

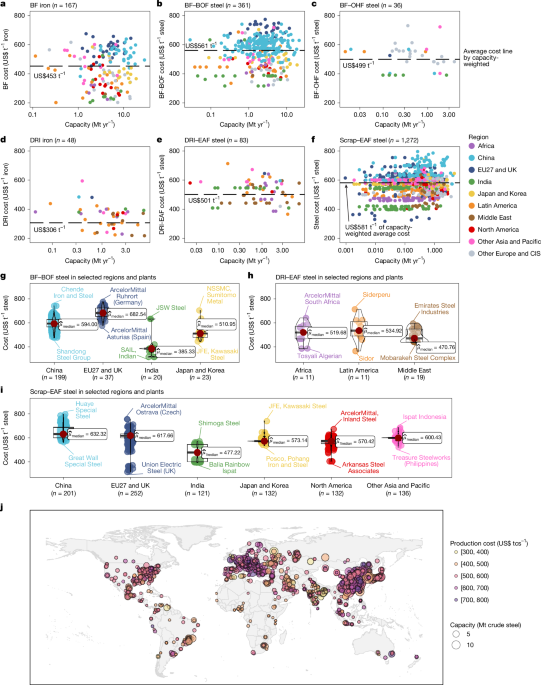
The World Crude Steel Capacity and Production Database³⁸ (https://www.steelonthenet.com/plant.html) covers more than 4,900 operating plants worldwide with a total of more than 20,000 facilities in 127 countries. Of these, 1,967 plants are involved in the production of iron and crude steel, whereas the others are steel processing plants that are excluded from this study owing to their limited emissions and lack of decarbonization measures. The database contains facility-based information on processing routes, nominal capacities, start-up and retrofitting years, plant geographical locations, and ownership in the year 2018. The annual production of each plant has been updated for the years 2020 and 2021 according to the national steel production data from the World Steel Association (WSA) and the plant-level cost database below⁴⁸. This production database provides original information on technology types, capacity and operating ages of individual plants, which contributes to the differentiation of plant-specific decarbonization pathways.

The Global Iron and Steel Cost Database in this study is compiled and harmonized from the open database TransitionZero⁴⁷ (https://www.transitionzero.org/products/global-steel-cost-tracker) and the non-public Metalinfo steel cost database (http://www.metalinfo.cn). Access to the latter requires contacting the online customer service to purchase the database. The merged cost database encompasses the plant-level production costs of different processing routes for 1,082 global iron and steel plants in 2021. Cost information includes not only the total production cost per tonne of iron or crude steel but also four cost subcategories, that is, cost of raw materials, cost of energy and reductants, cost of labour and overheads, and capital charges. The database also provides geographical locations for each plant, facilitating the mapping between the cost database and the production database. Owing to data limitations, a group of small plants included in the production database are not covered in the cost database, accounting for 13% of global steel production⁴⁸. The production costs of these plants are estimated using the national capacity-weighted average costs for the same processing routes, ensuring consistency with the average costs of the majority of steel plants. We acknowledge that this approximation may introduce some uncertainty; however, it is a feasible approach given the limited availability of plant-level cost data.

CO₂ emissions of current and decarbonization technologies

The CO₂ emissions of current processing routes and decarbonization technologies are estimated using the mass balance approach of the WSA^10,49. Compared with the Intergovernmental Panel on Climate Change method, which requires historical emission factors measured from existing activities, the WSA’s approach based on the carbon balance of material flows is more suitable for estimating future emissions of yet-to-be-commercialized decarbonization technologies lacking empirical data^7,28,49,50. This method also enables emission estimation at the level of individual processes or facilities.

As shown in equation (1), the total CO₂ emissions of a steel plant are calculated as the sum of process-level emission intensities, each expressed per tonne of crude steel, multiplied by the plant’s crude steel output. The emission intensity of each process is obtained from the carbon content difference between purchased inputs and sold outputs, converted into CO₂ equivalents (equation (2)).

where E_total is the total CO₂ emissions of a steel plant, P is the total crude steel output of the plant, EI_i is the emission intensity of process i, normalized per tonne of crude steel, C_{i,purchased,j} is the amount of purchased feedstock j required in process i, normalized per tonne of crude steel, C_i,sold,k is the amount of sold product k from process i, normalized per tonne of crude steel, and EF_j and EF_k are the emission factors for items j and k, derived from the carbon content of materials using the stoichiometric ratio (44/12) to convert C into CO₂.

Calculations in this study incorporate Scope 1 and Scope 2 emissions. Scope 1 CO₂ emissions from process i include direct emissions from site chimneys (E_i,site) and CO₂ credits (E_i,credit) from on-site steam generation, as shown in equation (3). Scope 2 emissions refer to the indirect upstream emissions (E_i,upstream) related to electricity procurement (equation (4)).

Here process-based emission intensities for Scope 1 (EI_i,scope1) were collected from International Environmental Agency and previous studies^3,4,7,10, whereas emission intensities (EI_i,scope1+2) for each process in Scope 1 and Scope 2 were obtained from the WSA^49,51. The primary results in this study are based on Scope 1 emissions, whereas the impact of Scope 1 + 2 emissions are discussed in the sensitivity analyses (Supplementary Note 8 and Supplementary Table 7). The input and output flows (C_i) of current processing routes such as BF–BOF, DRI–EAF and Scrap–EAF were obtained from the WSA⁵², whereas those of 20 promising decarbonization technologies were collected from other literature^2,10,52 (Extended Data Table 1). Our estimates of emission intensities for existing steel plants and decarbonization technologies are comparable to previous research.

Future cost estimates of decarbonization technologies

A toolbox of 20 promising low-carbon and zero-carbon technologies for net-zero steel production has been developed^2,7,10,28 (Extended Data Fig. 2 and Extended Data Table Table 1). Estimating plant-specific dynamic costs of these options is essential to identify the least-cost technology solution for each plant. However, the early stage of most decarbonization technologies lack historical cost and capacity data, challenging traditional learning curve methods for cost forecast¹⁶. Therefore, we innovatively integrated global plant-level production and cost databases with a component-based cost forecasting model^16,53 and learning curves^32,40 of decarbonization components to project the plant-specific future costs for 20 decarbonization technologies (Supplementary Fig. 29).

According to the component-based method, the cost of a complex technology can be decomposed into the costs of its individual components at different levels of maturity¹⁶. For steel plants, conventional processing routes (that is, BF–BOF, DRI–EAF, Scrap–EAF and so on) have been commercialized for decades, with costs primarily driven by fluctuations in raw material and energy prices rather than by technological progress⁴⁷. By contrast, the technical maturity and future costs of novel decarbonization components (that is, CCS, carbon capture, utilization and storage (CCUS), bioenergy with carbon capture and storage (BECCS), H₂ and so on) in steel plants may change significantly with cumulative deployment experience and across regions^10,32,53. Therefore, the future production cost (Y) of a steel plant adopting a specific technology (k) can be divided into two parts:

where, Y_plant, Y_route and Y_novel represent the unit production costs (US$ tcs⁻¹) of the overall plant, processing routes and novel components, respectively; and i and j denote the types of conventional processing routes and novel components, respectively.

The cost of a processing route (Y_route) consists of four parts: the cost of raw materials (Y_{raw material}), including iron ore, scrap and coke; the cost of energy (Y_energy), such as thermal coal and electricity; the cost of labour and overheads (Y_labour); and the capital cost (Y_capital), as shown in equation (6). Plant-specific costs for each processing route across the 20 decarbonization options were calculated based on our plant-level cost database (Supplementary Note 3).

The cost of novel decarbonization components (Y_novel) was estimated using Wright’s law, postulating that the cost of technology (y_t) evolves as a function of cumulative capacity⁴⁰ (equations (7)–(9)).

where a_k,j represents the consumption factor of novel component j by technology k, expressed in units of j per tonne of crude steel; y_t,j denotes the cost of component j at time t (in US$ per unit of j); B_j is the initial cost at the first unit capacity, X_t,j is the cumulative capacity of component j by time t, b_j is a parametric constant and LR_j is the learning rate for component j. Technical consumption factors (a_k,j) of various decarbonization technologies were collected from previous studies^2,10. Values of B_j, LR_j and X_t,j for various novel components were obtained from historical databases and systematic literature reviews to ensure consistency. Supplementary Notes 3–5 describe the data sources (Supplementary Tables 2–4 and 8) and Supplementary Notes 9–10 outline the systematic review process (Supplementary Figs. 30–41 and Supplementary Tables 9–18). Regional variations in initial costs and cost reductions were carefully considered, provided relevant references were available.

By summing up the plant-specific cost of processing routes (Y_route) with the regional-varied future cost of novel components (Y_novel), we obtained the dynamic costs of 20 promising decarbonization technologies for each steel plant, laying a solid data foundation for subsequent plant-level economical pathway exploration. Several factors may influence future cost estimates, including initial costs, learning rates and cumulative capacities of novel components (for example, CCS and H₂), as well as price fluctuations of key raw materials and energy sources such as iron ore, scrap, coke and electricity (Supplementary Table 5). Sensitivity analyses of cost forecasts for all promising technologies with respect to 22 key factors were conducted (Supplementary Note 7).

Scenario design

Of all the technology transition options, we propose a bottom-up method to optimize plant-level net-zero pathways for global iron and steel plants, aiming to achieve retrofitting at the lowest production cost. In brief, each steel plant is assumed to undergo retrofitting every 20 years, consistent with the average capital investment cycle of steel equipment⁷. The construction period is simplified in this study owing to limited data availability. On the basis of the carbon-neutrality target years pledged by different countries, we estimate that all existing iron and steel plants would need to retrofit one to three times between now and their respective target years.

Without policy intervention (the reference scenario), only a few plants are expected to voluntarily implement efficiency improvements motivated by potential cost savings, yielding limited emission reductions. To achieve carbon neutrality, we consider three policy scenarios that enforce the deployment of decarbonization technologies by restricting the available technology options with varying levels of stringency. In all policy scenarios, steel plants are required to adopt zero-carbon technologies by the target net-zero year, but flexibility remains regarding when deployment begins. Specifically, the three scenarios are defined as: (1) early deployment, adopting zero-carbon technologies at the first retrofit; (2) medium deployment, adopting low-carbon technologies during the first few retrofits and zero-carbon technologies at the final retrofit; and (3) late deployment, retaining current technologies until the final retrofit, at which zero-carbon technologies are adopted.

To maximize the economic benefit of each plant, we assume that every plant can choose the lowest-cost technology option available at each retrofitting time under different policy scenarios. Sectoral-level changes, such as the potential increase in regional steel demand and the growing availability of scrap, are set as exogenous constraints based on International Energy Agency projections⁷ (Supplementary Fig. 3). In regions such as India, the Middle East, Africa and other Asian countries, where the establishment of new plants is needed to meet growing demand, the technology costs of new plants are assumed to be the national capacity-weighted average values. In regions with increasing scrap supply, whether a steel plant transitions to Scrap–EAF depends on whether Scrap–EAF is more cost-effective than other decarbonization options in that region. By aggregating all plant-level choices, we derive the least-cost global net-zero transition pathway. We also calculate the total CO₂ abatement potential and mitigation costs associated with this optimized pathway. The uncertainties in the optimal pathways, abatement potential and costs, arising from factors including technology cost forecasts, retrofitting cycles and energy transitions, are discussed in Supplementary Note 8 (Supplementary Table 6).

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.